随便说一说类型。

类型的作用

如果用记事本写一段程序，就会发现两个问题。

一个是没有代码提示，一个变量点另一个变量也不知道有没有拼写对。

另一个是很容易编译失败，因为可能会发生一些类型出错的问题。

有了类型能够避免手误，编辑器会提示不存在相应的成员变量，从而更早的发现问题。

使用类型可以显式地表达一种约束。比如加减乘除需要数字，如果传入了字符串就可以在编译期报错，而不是等到运行时才出错。

许许多多的类型组成了类型系统。类型系统按不同的维度可以分为好几种。

强类型和弱类型

如果一个类型系统允许隐式类型转换，就是弱类型。否则为强类型。

C 系列语言就是弱类型。它允许隐式类型转换，如整数类型转为浮点数类型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>

void printFloat(float v)
{
	printf("%f\n", v);
}

int main(void) 
{
	int i = 0;
	printFloat(i);        // 隐式类型转换
	printFloat((float)i); // 显式类型转换
	return 0;
}

Haskell 不允许隐式类型转换。

1
2
3
4
5
printFloat :: Float -> IO ()
printFloat v = putStrLn (show v)

main = do printFloat (toInteger 1)
          printFloat 1.0

会编译失败。报错类型不匹配

1
2
3
Couldn't match expected type ‘Float’ with actual type ‘Integer’
In the first argument of ‘printFloat’, namely ‘(toInteger 1)’
In a stmt of a 'do' block: printFloat (toInteger 1)

强类型看起似乎麻烦一些，但是类型转换的工作总是要做的。类型转换的规则应该按照实际情况来，是向下取整还是四舍五入。强类型逼迫思考这部分的逻辑，避免错误被隐藏。

动态类型和静态类型

如果类型能够在编译期确定，就是静态类型，否则为动态类型。

C 系列语言都是静态类型。举一个 C# 的例子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
using System;

public class Test
{
	public static void Main()
	{
		Console.WriteLine(PlusSecond(1));
	}
	
	public static int PlusSecond(int donation)
	{
		int life = int.MaxValue;
		return life + donation; // donation 一定是 int 类型
	}
}

大部分的脚本语言都是动态类型，比如又爱又恨的 JavaScript

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function PlusSecond(donation)
{
  var life = Infinity;
  console.log(typeof(donation)) // 运行时才能确定 donation 的类型。
  return life + donation;
}

// 甚至不能确定函数的返回类型
PlusSecond(1);
// => number
// => Infinity
PlusSecond(" life");
// => string
// => "Infinity life"

动态类型虽然不能确定类型但还是有类型的。

动态类型虽然没有类型，容易出错，但是有 REPL 可以快速迭代代码啊，撸起袖子就是干。只可惜动态一时爽，重构火葬场。

无类型

现在大部分的语言都是有类型的。毕竟有类型很方便啊。但还是存在一些无类型的语言，虽然可能算不上编程语言。

入演算（滑稽），Lambda Calculus，就是一种无类型的，与图灵机等价的计算模型。

语法为

1
2
3
<exp> ::= <var>
<exp> ::= (λ<var>.<exp>)
<exp> ::= (<exp> <exp>)

规约规则有 α-变换（重命名），β-归约（应用）和 η-变换（外延性相等）。

具体规则可以参考未来的我写的λ 演算。

从语法中没有看到半点关于类型的东西，甚至连循环都看不到。

没有循环还能不能愉快的写代码了。

循环可以用递归代替。那递归怎么实现呢？

虽然定义中没有给出递归，但是可以通过不动点组合子实现。

比如著名的 Y 组合子

$Y=\lambda f.(\lambda x.f\ (x\ x))\ (\lambda x.f\ (x\ x))$

利用不动点的性质就可以达到递归。

$Y\ g=g\ (Y\ g)=g\ (g\ (Y\ g))=g\ (\ldots g\ (Y\ g)\ldots )$

不过因为 Y 组合子是 Call by name。而传统的语言一般是立即求值，所以需要 Y 组合子的 Call by value 版 Z 组合子。

$Z=\lambda f.(\lambda x.f(\lambda v.xxv))(\lambda x.f(\lambda v.xxv))$

Z 组合子的用法很简单，比如在 ES6 中用递归的方式写阶乘

1
2
3
4
5
6
7
const Z = f => (x => f(v => x(x)(v)))
               (x => f(v => x(x)(v)))

const fact = Z (f => n => n == 1 ? 1 : n * f(n - 1))

fact(3)
// => 6

那么问题来了，Z 的类型是？

函数类型

在无类型的入演算引入蕴含（$\to$）就会变成简单类型的入演算（$\lambda^\to$）。

类型规则很简单

$\dfrac{}{x:\sigma \vdash x : \sigma}$

$\dfrac{\Gamma\vdash x:\sigma\quad x\not=y}{\Gamma,y:\tau \vdash x : \sigma}$

$\dfrac{\Gamma,x:\sigma\vdash t:\tau} {\Gamma\vdash \lambda x : \sigma.t : \sigma \to \tau}$

$\dfrac{\Gamma\vdash t:\sigma\to\tau\quad\Gamma\vdash u:\sigma}{\Gamma\vdash t\,u : \tau}$

例如组合子 IKS 的类型为

$\lambda x:\alpha.x : \alpha\to\alpha$ (I)

$\lambda x:\alpha.\lambda y:\beta.x:\alpha \to \beta \to \alpha$ (K)

$\lambda x:\alpha\to\beta\to\gamma.\lambda y:\alpha\to\beta.\lambda z:\alpha.x z (y z) : (\alpha\to\beta\to\gamma)\to(\alpha\to\beta)\to\alpha\to\gamma$ (S)

注意有不少类型是简单类型不能表达的。比如 call/cc 柯里-霍华德同构于皮尔士定律，这在直觉逻辑中是不成立的。所以 call/cc 不能居留。

函数类型是一种值依赖值的例子。

和类型与积类型

在简单类型的入演算（$\lambda^\to$）引入类型操作符就会变成带类型操作符的简单类型入演算（$\lambda\underline\omega$）

普通的函数是一种操作值的操作符。

类似的，接收类型为参数返回类型的函数成为类型操作符。

有很多类型操作符，所以也会产生很多类型。这里主要提两种类型和类型与积类型。

很多编程语言使用 null 或者类似的原语来表达缺少值的情况。

但这会有两个问题。

一个是 null 只适用于引用类型，如果是值类型比如 int ，那么该怎么表示缺少值的情况呢？

有些人会取一个范围外的值比如对于输入一定是整数的情况的下可以取 -1 用于表达缺少值。

在输入包含负数的情况下不能用，这就很尴尬了。

值类型还好，错误的输入最多是得到错误的值，而引用类型就不一样了。

如果使用了 null 就必须检查，否则可能会因为空引用而崩溃。

而且使用了 null 相当于绕过了类型系统的检查，是不是 null 只能在运行时确定，做不到检查出 null 而编译失败。

理论上只要做了空检查就不会有问题，但是在复杂的数据结构嵌套中很容易就忘了对某个成员的检查。

这样的感觉像是写动态类型一样，觉得应该是没问题的，最后运行代码然后祈祷不要出错。

Haskell 中使用 Maybe 类型操作符来表达缺少值的情况。

1
data Maybe a = Nothing | Just a  -- a 为类型参数

注意到 a 为类型变量，可以是 Int，String，Char 等。例如

1
2
3
4
5
6
7
8
ghci> Just "Haha"  
Just "Haha"  
ghci> Just 84  
Just 84  
ghci> :t Just "Haha"  
Just "Haha" :: Maybe [Char]  
ghci> :t Just 84  
Just 84 :: (Num t) => Maybe t

使用 Maybe 必须检查是否为 Nothing 否则编译失败。不过检查的过程是自动的（多亏了 Monad 和 do-notation）。

引入 null 不是错误，错误的是没有强制检查 null （C# 可以使用 ?. 和 ?? 简化检查）。

当 a 为 Int 时 Maybe 返回 Maybe Int 。

Maybe Int 是什么类型呢。其实是一种和类型，是 Int + Nothing 。

所以 Maybe 之所以能表达缺少值的情况是因为它可以容纳两种类型。

类似的，积类型可以用 (,) 操作符或者 std::pair 生成。

$(A, B)$ 的类型是 A 类型和 B 类型的笛卡儿积 $A \times B$ 。

类型操作符是一种类型依赖类型的例子。

多态类型

在简单类型的入演算（$\lambda^\to$）引入全称量词（$\forall$）就会变成二阶入演算（$\lambda2$），又称为系统 F 。

引入 $\forall$ 后获得多态的能力。系统 F 的多态是参数化多态。

参数化多态类似于泛型。比如对于 List<T> 有

$length: \forall T.[T] \to int$

注意到 length 是 Rank-1 类型。但有的函数可能是 Rank-2 类型。

比如 $(\forall a.a \to a) \to (\forall b.b \to b)$ 就是 Rank-2 类型。

但不是有 N 个全称量词就是 Rank-N 类型。

$\forall a. a \to (\forall b.b \to a)$ 是 Rank-1 类型。

因为可以规约为 $\forall a b . a \to b \to a$ 。

通常的类型系统是 Rank-1 类型。系统 F 支持 Rank-N 类型。

Haskell 的类型系统 Hindley–Milner 类型系统是一种带类型类的系统 F 。默认是 Rank-1 ，需要手动开启 Rank-N 。

比如要使用代替 getter / setter 的光学棱镜组就要开启 Rank-N 。

除了参数化多态，还有特设多态。

特设多态是指一个多态函数有多种实现，依赖于参数的类型，调用相应的版本，类似于面向对象中的重载（overload）。

所以特设多态只能支持有限数量的类型。而参数化多态更为通用。

多态类型是一种值依赖类型的例子。

依赖类型

容器类型除了元素类型还跟长度有关，不同长度的同元素类型构成了一个容器簇。

如果把长度当作容器类型构造器的参数，那么就形成了依赖类型。

依赖类型分为依赖乘积类型（Π-类型）和依赖总和类型（Σ-类型）。

依赖乘积类型可以写作 $\displaystyle \Pi (x:A),B(x)$ ，当 $B$ 为常数时，即 $\displaystyle \Pi {(x:A)},B$ ，退化为函数类型 $A \to B$

依赖总和类型可以写作 $\displaystyle \Sigma {(x:A)},B(x)$ ，当 $B$ 为常数时，即 $\displaystyle \Sigma {(x:A)},B$ ，退化为乘积类型 $A \times B$

依赖类型使得容器类型长度变成了一种约束。

例如对于元素类型为 T，长度为 n 的 List 类型 $List(T,n)$ ，它的 append 操作类型为

$append : List(T,n) \to List(T,m) \to List(T,m + n)$

如果最后返回值长度不是 $m+n$ 就会被编译器踢屁股，编译失败。

这样尽可能用类型表达更多的约束，将逻辑问题扑灭在编译期，就能写出更正确的程序。

毕竟业务逻辑应该写在函数类型里，你之所以要写函数实现是因为编译器还没有聪明到自动做 $\beta$ 规约啊科科。

依赖类型是一种类型依赖值的例子。

这样就集齐了值和类型的四种关系。

简单类型($\lambda^\to$)是值依赖值的关系。

带类型操作符的简单类型($\lambda\underline\omega$)是类型依赖类型的关系。

二阶入演算（$\lambda2$）是值依赖类型的关系。

依赖类型（$\lambda P$）是类型依赖值的关系。

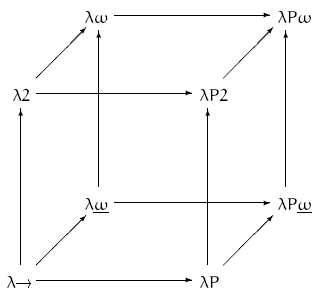
以 $\lambda^\to$ 为原点，其他三种关系为基底，就得到了常见类型系统的入立方。

入立方